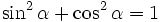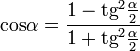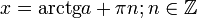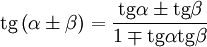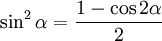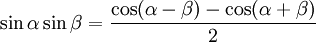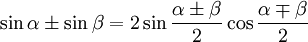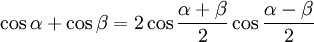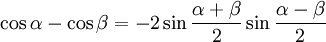Основные тригонометрические тождества

 

Основные тригонометрические формулы

 

Основные формулы
	(1)
	(2)
	(3)

Формула (1) является следствием теоремы Пифагора.

Формулы сложения аргументов

 

Формулы сложения аргументов
	(5)
	(6)
	(7)

Формула (7) получается при делении (5) на (6).

 

Вывод формул   

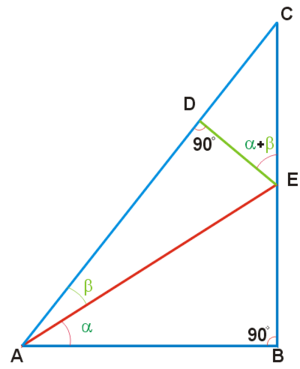
На Рис. 4 изображены четыре прямоугольных треугольника: ABC, ABE, ADE и CDE.

Рис. 4. К выводу формул суммы углов

Принято, что AE = 1, .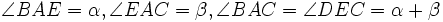

Так как AE = 1, то

(BE) = sin?

(AB) = cos?

(DE) = sin?

(AD) = cos?.

Из треугольника ABC следует:

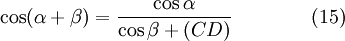
Из треугольника CDE следует:

.

Приравниваем правые части уравнений (14) и (16):

Приравниваем правые части уравнений (15) и (17) и решаем, полученное уравнение относительно CE:

.

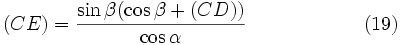Подставляем (CE) из (19) в (18):

.

Полученное значение для CD подставляем в (15):

.

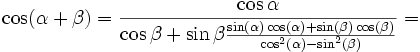
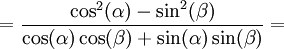
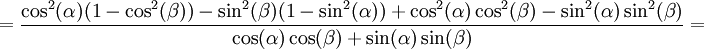
Итак:

cos(? + ?) = cos(?)cos(?) ? sin(?)sin(?).

Из формулы (15) следует:

Из формулы (16) и (17) следует:

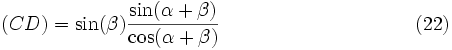
Приравниваем правые части (21) и (22) и находим sin(? + ?):

Подставляем значение cos(? + ?):

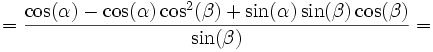
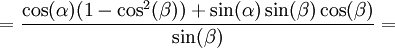
Итак:

sin(? + ?) = sin(?)cos(?) + cos(?)sin(?).

 Формулы двойного угла

 

Формулы двойного угла выводятся из формул (5), (6) и (7), если принять, что угол ? равен углу ?:

Формулы двойного угла
sin2? = 2sin(?)cos(?)	(23)
cos2? = cos2? ? sin2? = 2cos2? ? 1 = 1 ? 2sin2?	(24)
	(25)

Формулы понижения степени

 

Формулы понижения степени выводятся из формулы (24), заменой cos²? = 1 ? sin²? и sin²? = 1 ? cos²?:

Формулы понижения степени
	(26)
	(27)

Формулы преобразования произведений функций

 

Формулы преобразования произведений функций
	(28)
	(29)
	(30)

Вывод формул преобразования произведений функций  

Формулы сложения функций выводятся из формул сложения аргументов (5), (6) и (7). Например, из формулы (5) следует:

sin(? + ?) + sin(? ? ?) = sin?cos? + cos?sin? + sin?cos? ? cos?sin? =

= 2sin?cos?.

То есть:

   — формула (29).

Остальные формулы преобразования произведений функций выводятся аналогично.

Формулы преобразования суммы функций

 

Формулы преобразования суммы функций
	(31)
	(32)
	(33)
	(34)
	(35)

Авторы: Ефремова Юля и Ерниязова Вера.