| ||||||
|
| |||||
Тригонометрические функцииКосинусом угла ? называется абсцисса x точки B ? конца радиус-вектора единичной окружности, образующего угол ? с осью абсцисс.
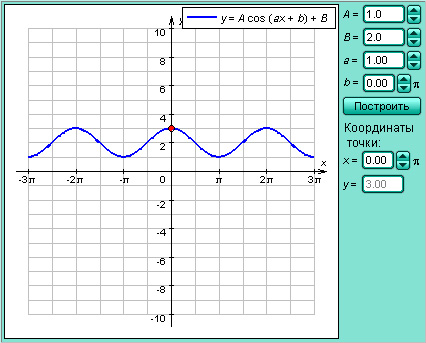
Модель 2.8. Функция y = cos x
Синусом угла ? называется ордината y точки B ? конца радиус-вектора единичной окружности, образующего угол ? с осью абсцисс.
Модель 2.7. Функция y = sin x
Тангенсом угла ? называется отношение ординаты y к абсциссе x точки B ? конца радиус-вектора единичной окружности, образующего угол ? с осью абсцисс.
Модель 2.9. Функция y = tg x
Котангенсом угла ? называется отношение абсциссы x к ординате y точки B ? конца радиус-вектора единичной окружности, образующего угол ? с осью абсцисс.
Модель 2.10. Функция y = ctg x Ясно, что для данного угла ? функции sin ?, cos ?, tg ? и ctg ?, которые называются тригонометрическими функциями , определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin ? и cos ? определены для любого угла ?, то функции tg ? и ctg ? определены только для тех углов, для которых не равен нулю знаменатель дробей Поскольку синус по определению равен ординате точки на единичной окружности, а косинус ? абсциссе, то знаки тригонометрических функций по четвертям будут такими: Функция Знаки тригонометрических функций по четвертям I II III IV sin ? + + ? ? cos ? + ? ? + tg ? + ? + ? ctg ? + ? + ? Таблица 2.4.1.2 Рисунок 2.4.1.3. Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов. Конец радиус-вектора, отвечающего углу 0°, точка A , имеет координаты (1; 0). Поэтому cos 0° = 1, sin 0° = 0, tg 0° = 0, ctg 0° не определён. Совершенно аналогично рассматриваются точки B (0; 1), C (–1; 0) и D (0; –1), что даёт: sin 90° = 1, cos 90° = 0, ctg 90° = 0, tg 0° не определён. sin 180° = 0, cos 180° = –1, tg 180° = 0, ctg 180° не определён. sin 270° = –1, cos 270° = 0, ctg 270° = 0, tg 270° не определён. Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе: Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка O – совпадёт с началом координат, а точка A будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу OA = 1), то геометрическое определение синуса примет вид: Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением. Рисунок 2.4.1.4. Рисунок 2.4.1.5. Рассмотрим правильный треугольник ABC со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты BH равна Рисунок 2.4.1.6. Значит, Рассмотрим теперь прямоугольный равнобедренный треугольник ABC с катетами, равными CA = CB = 1, Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили. Функция Углы 0° 30° 45° 60° 90° 180° 270° 360° Градусы 0° Пример 2 Найдите значения выражений 1) 2) Показать решение Имеем: 1) 2) Ответ. 1) 1; 2)
Функция f называется периодической с периодом T ? 0, если для любого x из области определения функции выполнено: Если функция f имеет период T , то она, очевидно, имеет период nT , где Пример 3 Доказать, что НПП функции y = sin x является 2?. Показать решение Из определения функции следует, что у точек x и x + 2? одинаковая ордината, следовательно, sin x = sin ( x + 2?), а это означает, что 2? является периодом функции sin x . Пусть T ? некоторый период функции y = sin x . Тогда для всех x должно выполняться равенство sin x = sin ( x + T ). При x = 0 имеем sin T = 0. Значит, T может принимать значения только ? n , где
Аналогично можно показать, что функция y = cos x также имеет НПП T = 2?. А функции y = tg x и y = ctg x имеют НПП T = ?. | ||||||
|
| ||||||
| НАЦИОНАЛЬНЫЙ ФОНД ПОДГОТОВКИ КАДРОВ. ИНФОРМАТИЗАЦИЯ СИСТЕМЫ ОБРАЗОВАНИЯ. Сайт сделан по технологии "Конструктор школьных сайтов". | ||||||


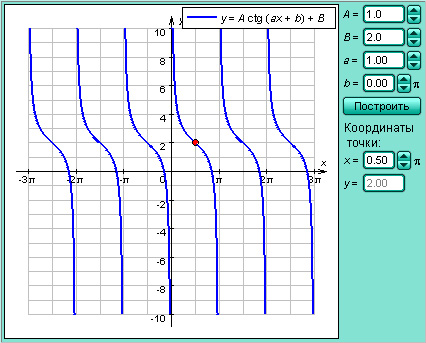
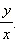 Значит, tg ? не определён для углов вида
Значит, tg ? не определён для углов вида 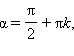 где
где 

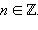 Поэтому говорят о
Поэтому говорят о  Значит, НПП функции
Значит, НПП функции